Why Infrared Heat?
Why Infrared Heat?
Why Infrared Heat?
Why Infrared Heat?
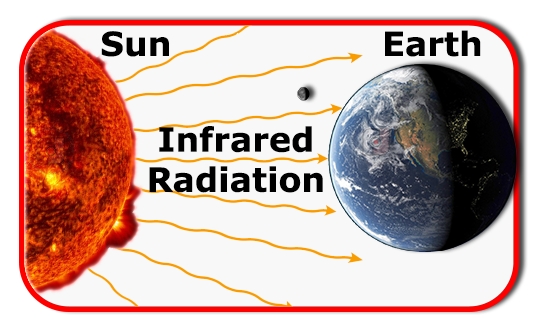
This patented feature of the Reflect-O-Ray® and Omega II® systems increases the efficiency of our radiant tube systems. Our patented Low Mass radianRadiant Infrared energy is the oldest form of heating used to provide heating comfort. Radiant tube heaters deliver the heat to the ground level verses heating the surrounding air. Using a Radiant Tube Heater takes advantage of this principle, heating like the sun. The radiant energy that is radiated from the radiant tube heater is absorbed by floor and objects within a room without physical contact with the heat source.
The heating of the air within a building when using radiant tube heater is primarily done by the largest mass or heat sink in a building, the floor. Additional heating benefits are provided by the other masses with in a building tables, inventory, cars, etc… This method of heating keeps the heat where you need it down by the floor. This all translates into better comfort, more efficient heating, and a lower cost of heating.t tubing heats up faster, allowing optimum radiant emitter output faster than any other radiant tube systems available.
Step One
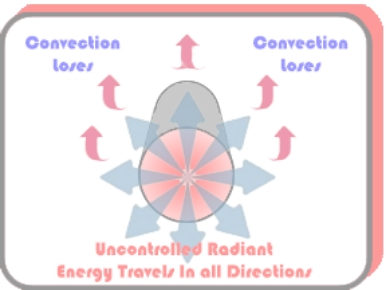
Step Two
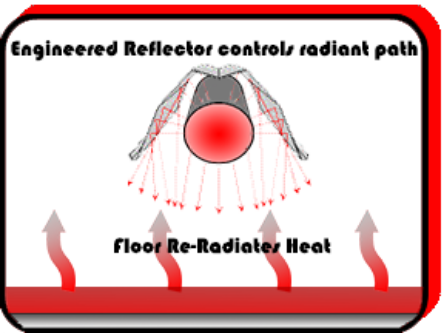
Step Three
Systems that take advantage of this principle are the OMEGA II and REFLECT-O-RAY Radiant infrared heating systems. You can find a representative by clicking here or if you are looking for specifications for radiant heating tubes click here for Omega II radiant tube heater specifications or click here for Reflect-O-Ray tube heater specifications.
Radiant tube heaters operate by vacuum (negative) or power (positive) pressure. The radiant energy produced is then directed downward by the reflectors positioned above the radiant tubes. In general vacuum pressure systems are more efficient than Power pressure systems
This patented feature of the Reflect-O-Ray® and Omega II® systems increases the efficiency of our radiant tube systems. Our patented Low Mass radianRadiant Infrared energy is the oldest form of heating used to provide heating comfort. Radiant tube heaters deliver the heat to the ground level verses heating the surrounding air. Using a Radiant Tube Heater takes advantage of this principle, heating like the sun. The radiant energy that is radiated from the radiant tube heater is absorbed by floor and objects within a room without physical contact with the heat source.
The heating of the air within a building when using radiant tube heater is primarily done by the largest mass or heat sink in a building, the floor. Additional heating benefits are provided by the other masses with in a building tables, inventory, cars, etc… This method of heating keeps the heat where you need it down by the floor. This all translates into better comfort, more efficient heating, and a lower cost of heating.t tubing heats up faster, allowing optimum radiant emitter output faster than any other radiant tube systems available.
Step One

Step Two

Step Three
Systems that take advantage of this principle are the OMEGA II and REFLECT-O-RAY Radiant infrared heating systems. You can find a representative by clicking here or if you are looking for specifications for radiant heating tubes click here for Omega II radiant tube heater specifications or click here for Reflect-O-Ray tube heater specifications.
Radiant tube heaters operate by vacuum (negative) or power (positive) pressure. The radiant energy produced is then directed downward by the reflectors positioned above the radiant tubes. In general vacuum pressure systems are more efficient than Power pressure systems


